LOS PUENTES DE KÖNIGSBERG

Königsberg fue una popular y rica cuidad de la Prusia Oriental, hoy en día su nombre es Kaliningrado y pertece a Rusia, se encuentra a orillas del mar Báltico y a unos 50 km de la frontera con Polonia.

En esta ciudad se juntan dos ríos, formando una isla en su confluencia. Siete puentes unían (ya no, pues la ciudad fue parcialmente destruida durante la segunda Guerra Mundial) las diferentes partes de la ciudad, como se aprecia en el mapa de la época. En el siglo XVIII se hizo popular como adivinanza/pasatiempo averiguar si era posible cruzar los siete puentes de la ciudad pasando sólo una vez por cada uno de ellos.

Königsberg en tiempos de Euler

Kaliningrado, en la actualidad

Esta ciudad es conocida también por ser la cuna del filósofo Immanuel Kant (1724 - 1804), pero en la historía de las Matemáticas es famosa por la disposición de sus puentes que dió lugar a este juego, precisamente en la época de Kant, que atrajo la atención de los más famosos matemáticos del momento.

Este problema, por supuesto, puede resolverse mediante un estudio exhaustivo de todos los posibles itineriarios. Pero en las matemáticas nos interesamos por generalizar el problema y buscar una solución sencilla y válida para todos los posibles mapas de ciudades, e incluso objetos más generales.

En 1736, el gran matemático suizo afincado en San Petersburgo, Leonhard Euler, publicó su "Solutio problematis ad geometriam situs pertinentis", un artículo en el que resolvía el problema en el caso general. Este trabajo es considerado como en el nacimiento de la Teoría de Grafos, utilizada hoy en día en un sinfín de aplicaciones, y también uno de las primeras apariciones de una "nueva Geometría" en la que importan sólo las propiedades estructurales de un objeto y no sus medidas. A esto se refieren las palabras "geometrian situs" en el título de Euler, palabras que hoy se traducen como Topología.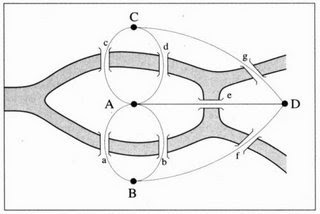

La primera observación es que el problema se puede reformular como sigue. Dado el siguiente "grafo" con cuatro vértices y siete aristas, ¿es posible recorrerlo entero sin pasar dos veces por la misma arista?. En el grafo, los cuatro vértices representan las cuatro partes en que los ríos separan la ciudad, y las siete aristas representan los puentes. Dicho de otro modo, que resulte más familiar a los aficcionados de los pasatiempos: ¿es posible realizar el dibujo del grafo sin levantar el lápiz del papel y sin pasar dos veces por la misma arista? (Se permite pasar dos veces por el mismo vértice).


La respuesta de Euler es extremadamente simple. Supongamos que, efectivamente, es posible realizar el dibujo sin levantar el lápiz del papel. Al realizar el dibujo, en cada vértice intermedio que atravesemos entraremos por una arista y saldremos por otra. En particular, el número de aristas que confluyen en cada vértice del grafo, exceptuando quizás los vértices inicial y final del dibujo, ha de ser par. Si llamamos "valencia" de cada vértice al número de aristas que confluyen en él, lo dicho anteriormente significa que para que el problema tenga solución es necesario que en el grafo haya como mucho dos vértices de valencia par. En el caso del grafo de Königsberg los cuatro vértices tienen valencia impar, así que el problema no tiene solución. Q.E.D.