 La navidad según Mafalda, siempre me ha gustado mucho su humor y su forma de ver el mundo, así que aquí os dejo una tira cómica... para deciros:
La navidad según Mafalda, siempre me ha gustado mucho su humor y su forma de ver el mundo, así que aquí os dejo una tira cómica... para deciros:sábado, 20 de diciembre de 2008
¡FELIZ NAVIDAD!
 La navidad según Mafalda, siempre me ha gustado mucho su humor y su forma de ver el mundo, así que aquí os dejo una tira cómica... para deciros:
La navidad según Mafalda, siempre me ha gustado mucho su humor y su forma de ver el mundo, así que aquí os dejo una tira cómica... para deciros:viernes, 28 de noviembre de 2008
DE VUELTA
Después de dejar aparcado el blog durante todas las vacaciones de verano, el regreso se ha hecho más largo de lo esperado por todo lo que supone un comienzo de curso y adaptarnos a la rutina, pero como podéis ver aquí estoy de vuelta, con intención de colgar nuevos e interesantes posts. De momento, hoy os dejo uno cortito.
 En alguna ocasión me habéis preguntado el tema de dejar comentarios, es muy sencillo, al final de cada post, veréis a la derecha que pone tantos comentarios, pincháis ahí y se os abre una ventanita donde dice Haga su comentario (en el hueco en blanco), en Elegir una identidad, como no todo el mundo es blogger o tiene cuenta en gmail, os podéis ir a la tercera opción Nombre/URL (lo del URL olvidaros también) o la última opción Anónimo y firmáis dentro del comentario mismo.
En alguna ocasión me habéis preguntado el tema de dejar comentarios, es muy sencillo, al final de cada post, veréis a la derecha que pone tantos comentarios, pincháis ahí y se os abre una ventanita donde dice Haga su comentario (en el hueco en blanco), en Elegir una identidad, como no todo el mundo es blogger o tiene cuenta en gmail, os podéis ir a la tercera opción Nombre/URL (lo del URL olvidaros también) o la última opción Anónimo y firmáis dentro del comentario mismo.
 Por hoy para terminar, os dejo con un video para recordaros que las Matemáticas están detrás de todo, por cierto para los alumnos de 3º ESO habla de nuevo de la famosa sucesión de Fibonacci, la cual ya apareció en anteriores posts y lo hemos visto este trimestre en clase, espero os guste y hasta muy prontito.
Por hoy para terminar, os dejo con un video para recordaros que las Matemáticas están detrás de todo, por cierto para los alumnos de 3º ESO habla de nuevo de la famosa sucesión de Fibonacci, la cual ya apareció en anteriores posts y lo hemos visto este trimestre en clase, espero os guste y hasta muy prontito.
 En alguna ocasión me habéis preguntado el tema de dejar comentarios, es muy sencillo, al final de cada post, veréis a la derecha que pone tantos comentarios, pincháis ahí y se os abre una ventanita donde dice Haga su comentario (en el hueco en blanco), en Elegir una identidad, como no todo el mundo es blogger o tiene cuenta en gmail, os podéis ir a la tercera opción Nombre/URL (lo del URL olvidaros también) o la última opción Anónimo y firmáis dentro del comentario mismo.
En alguna ocasión me habéis preguntado el tema de dejar comentarios, es muy sencillo, al final de cada post, veréis a la derecha que pone tantos comentarios, pincháis ahí y se os abre una ventanita donde dice Haga su comentario (en el hueco en blanco), en Elegir una identidad, como no todo el mundo es blogger o tiene cuenta en gmail, os podéis ir a la tercera opción Nombre/URL (lo del URL olvidaros también) o la última opción Anónimo y firmáis dentro del comentario mismo. Por hoy para terminar, os dejo con un video para recordaros que las Matemáticas están detrás de todo, por cierto para los alumnos de 3º ESO habla de nuevo de la famosa sucesión de Fibonacci, la cual ya apareció en anteriores posts y lo hemos visto este trimestre en clase, espero os guste y hasta muy prontito.
Por hoy para terminar, os dejo con un video para recordaros que las Matemáticas están detrás de todo, por cierto para los alumnos de 3º ESO habla de nuevo de la famosa sucesión de Fibonacci, la cual ya apareció en anteriores posts y lo hemos visto este trimestre en clase, espero os guste y hasta muy prontito.miércoles, 18 de junio de 2008
PHI, EL NÚMERO DE ORO

 Phi, el número de oro o número áureo, famoso a lo largo de la historia, ha sido y es para muchos símbolo de belleza, magia, perfección, divinidad, ... en este post os cuento todo sobre él.
Phi, el número de oro o número áureo, famoso a lo largo de la historia, ha sido y es para muchos símbolo de belleza, magia, perfección, divinidad, ... en este post os cuento todo sobre él. Para empezar una práctica muy sencilla, coge una tarjeta de crédito o tu DNI, una postal, una foto carnet,... y divide el largo entre el ancho, como podrás comprobar casi siempre el cociente es un número próximo a 1,618... No es casualidad, este es el número de oro y desde tiempos muy remotos se ha considerado como la proporción largo-ancho ideal (razón áurea), por ello, que muchos de los objetos en la actualidad se rigan por ésta.
Para empezar una práctica muy sencilla, coge una tarjeta de crédito o tu DNI, una postal, una foto carnet,... y divide el largo entre el ancho, como podrás comprobar casi siempre el cociente es un número próximo a 1,618... No es casualidad, este es el número de oro y desde tiempos muy remotos se ha considerado como la proporción largo-ancho ideal (razón áurea), por ello, que muchos de los objetos en la actualidad se rigan por ésta.Pero vayamos por partes, algebráicamente, si resolvemos la siguiente ecuación:
x2=x+1
pasamos todos los términos a un lado,
x2-x-1=0
y la resolvemos, resulta:
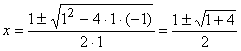
Tomando la solución positiva, obtenemos:
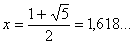
y la resolvemos, resulta:
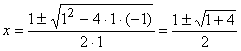
Tomando la solución positiva, obtenemos:
Este número irracional (infinitos decimales no periódico) es conocido como número de oro, abreviadamente, Phi, en honor al escultor Phidias, que tanto lo utilizó, se representa con dicha letra griega, que es la inicial de Phidias en griego.
 Este número es tan famoso, porque desde la Grecia antigua, pasando por los romanos, los artistas del renacimiento y llegando a los pintores, escultores, arquitectos, ... actuales, ha sido considerado como la proporción ideal y canon de belleza, por lo que lo han utilizado para múltiples construcciones y obras de arte... Pero también se ha observado la presencia de éste en la naturaleza, la geometría, etc.
Este número es tan famoso, porque desde la Grecia antigua, pasando por los romanos, los artistas del renacimiento y llegando a los pintores, escultores, arquitectos, ... actuales, ha sido considerado como la proporción ideal y canon de belleza, por lo que lo han utilizado para múltiples construcciones y obras de arte... Pero también se ha observado la presencia de éste en la naturaleza, la geometría, etc.
 El Partenón de Atenas, es un claro ejemplo de construcción en la que podemos encontrar este famoso rectángulo de oro en diferentes partes. Otro ejemplo de construcción que sigue esta razón es la catedral de Notre Dame de París, veáse la foto.
El Partenón de Atenas, es un claro ejemplo de construcción en la que podemos encontrar este famoso rectángulo de oro en diferentes partes. Otro ejemplo de construcción que sigue esta razón es la catedral de Notre Dame de París, veáse la foto.
 ¿Sorprendido?, pues aún hay más, los grandes pintores del renacimiento, ya conocían este
¿Sorprendido?, pues aún hay más, los grandes pintores del renacimiento, ya conocían este secreto, pongamos de ejemplo a Leonardo da Vinci y su famosa Gioconda, sí, el cuadro más famoso del mundo, fue pintado siguiendo las reglas de este rectángulo mágico; otra de sus obras, el famoso Hombre de Vitruvio, también sigue dichas proporciones, de hecho se consideraba que una persona era matemáticamente perfecta si su altura y la distancia desde el suelo al ombligo estaban en proporción áurea... lo se, no todos podemos ser matemáticamente perfectos, aunque casi, haz la prueba y comprobarás que te aproximas bastante al número.
secreto, pongamos de ejemplo a Leonardo da Vinci y su famosa Gioconda, sí, el cuadro más famoso del mundo, fue pintado siguiendo las reglas de este rectángulo mágico; otra de sus obras, el famoso Hombre de Vitruvio, también sigue dichas proporciones, de hecho se consideraba que una persona era matemáticamente perfecta si su altura y la distancia desde el suelo al ombligo estaban en proporción áurea... lo se, no todos podemos ser matemáticamente perfectos, aunque casi, haz la prueba y comprobarás que te aproximas bastante al número.

 El número de oro está íntimamente ligado al pentágono regular y estrella de cinco puntas (símbolo de la escuela de Pitágoras, que también ya lo conocía por entonces), pues el cociente AD/AB da de nuevo como resultado el número de oro, en la foto, podemos apreciarlo en La Sagrada Familia de Miguel Ángel.
El número de oro está íntimamente ligado al pentágono regular y estrella de cinco puntas (símbolo de la escuela de Pitágoras, que también ya lo conocía por entonces), pues el cociente AD/AB da de nuevo como resultado el número de oro, en la foto, podemos apreciarlo en La Sagrada Familia de Miguel Ángel.
 Comentaba antes la presencia también de esta proporción en la naturaleza, una de las más bellas y conocidas es el caso del Nautilus (molusco en espiral), de ahí que se conozca como espiral áurea.
Comentaba antes la presencia también de esta proporción en la naturaleza, una de las más bellas y conocidas es el caso del Nautilus (molusco en espiral), de ahí que se conozca como espiral áurea.


 En un post anterior hablé de la estrecha relación entre el número de oro y la sucesión de Fibonacci, ambas presentes en múltiples fenómenos de la naturaleza, por ejemplo, los girasoles cuentan con dos series de espirales que salen del centro (una en cada sentido), 21 en un sentido y 34 en el otro, números que se extraen de la famosa sucesión.
En un post anterior hablé de la estrecha relación entre el número de oro y la sucesión de Fibonacci, ambas presentes en múltiples fenómenos de la naturaleza, por ejemplo, los girasoles cuentan con dos series de espirales que salen del centro (una en cada sentido), 21 en un sentido y 34 en el otro, números que se extraen de la famosa sucesión.

 ¿Casualidad?. No, matemáticas, y es que la naturaleza es sabia. Según vas realizando los cocientes de los términos de la sucesión de Fibonacci, observarás, que cada vez se aproxima más y más al número de oro. Anecdotas y ejemplos hay miles y ya me está quedando un post de lo más largo y no quiero resultar pesado, sólo deciros que dicha proporción se sigue utilizando en la actualidad, por considerarse ideal, como mencioné antes, nuestro famoso DNI está en proporción áurea.
¿Casualidad?. No, matemáticas, y es que la naturaleza es sabia. Según vas realizando los cocientes de los términos de la sucesión de Fibonacci, observarás, que cada vez se aproxima más y más al número de oro. Anecdotas y ejemplos hay miles y ya me está quedando un post de lo más largo y no quiero resultar pesado, sólo deciros que dicha proporción se sigue utilizando en la actualidad, por considerarse ideal, como mencioné antes, nuestro famoso DNI está en proporción áurea.
 Ya véis, el número de oro, sigue presente en nuestro arte más actual, nuestro desaparecido genio Salvador Dalí, por ejemplo, lo utilizó para algunas de sus obras y se seguirá utilizando en generaciones futuras, por ser considerado un número mágico.
Ya véis, el número de oro, sigue presente en nuestro arte más actual, nuestro desaparecido genio Salvador Dalí, por ejemplo, lo utilizó para algunas de sus obras y se seguirá utilizando en generaciones futuras, por ser considerado un número mágico.
 Os dejo con un par de videos en los que podéis informaros un poco más sobre este fascinante número.
Os dejo con un par de videos en los que podéis informaros un poco más sobre este fascinante número.
 Este número es tan famoso, porque desde la Grecia antigua, pasando por los romanos, los artistas del renacimiento y llegando a los pintores, escultores, arquitectos, ... actuales, ha sido considerado como la proporción ideal y canon de belleza, por lo que lo han utilizado para múltiples construcciones y obras de arte... Pero también se ha observado la presencia de éste en la naturaleza, la geometría, etc.
Este número es tan famoso, porque desde la Grecia antigua, pasando por los romanos, los artistas del renacimiento y llegando a los pintores, escultores, arquitectos, ... actuales, ha sido considerado como la proporción ideal y canon de belleza, por lo que lo han utilizado para múltiples construcciones y obras de arte... Pero también se ha observado la presencia de éste en la naturaleza, la geometría, etc. El Partenón de Atenas, es un claro ejemplo de construcción en la que podemos encontrar este famoso rectángulo de oro en diferentes partes. Otro ejemplo de construcción que sigue esta razón es la catedral de Notre Dame de París, veáse la foto.
El Partenón de Atenas, es un claro ejemplo de construcción en la que podemos encontrar este famoso rectángulo de oro en diferentes partes. Otro ejemplo de construcción que sigue esta razón es la catedral de Notre Dame de París, veáse la foto. ¿Sorprendido?, pues aún hay más, los grandes pintores del renacimiento, ya conocían este
¿Sorprendido?, pues aún hay más, los grandes pintores del renacimiento, ya conocían este secreto, pongamos de ejemplo a Leonardo da Vinci y su famosa Gioconda, sí, el cuadro más famoso del mundo, fue pintado siguiendo las reglas de este rectángulo mágico; otra de sus obras, el famoso Hombre de Vitruvio, también sigue dichas proporciones, de hecho se consideraba que una persona era matemáticamente perfecta si su altura y la distancia desde el suelo al ombligo estaban en proporción áurea... lo se, no todos podemos ser matemáticamente perfectos, aunque casi, haz la prueba y comprobarás que te aproximas bastante al número.
secreto, pongamos de ejemplo a Leonardo da Vinci y su famosa Gioconda, sí, el cuadro más famoso del mundo, fue pintado siguiendo las reglas de este rectángulo mágico; otra de sus obras, el famoso Hombre de Vitruvio, también sigue dichas proporciones, de hecho se consideraba que una persona era matemáticamente perfecta si su altura y la distancia desde el suelo al ombligo estaban en proporción áurea... lo se, no todos podemos ser matemáticamente perfectos, aunque casi, haz la prueba y comprobarás que te aproximas bastante al número.
 El número de oro está íntimamente ligado al pentágono regular y estrella de cinco puntas (símbolo de la escuela de Pitágoras, que también ya lo conocía por entonces), pues el cociente AD/AB da de nuevo como resultado el número de oro, en la foto, podemos apreciarlo en La Sagrada Familia de Miguel Ángel.
El número de oro está íntimamente ligado al pentágono regular y estrella de cinco puntas (símbolo de la escuela de Pitágoras, que también ya lo conocía por entonces), pues el cociente AD/AB da de nuevo como resultado el número de oro, en la foto, podemos apreciarlo en La Sagrada Familia de Miguel Ángel. Comentaba antes la presencia también de esta proporción en la naturaleza, una de las más bellas y conocidas es el caso del Nautilus (molusco en espiral), de ahí que se conozca como espiral áurea.
Comentaba antes la presencia también de esta proporción en la naturaleza, una de las más bellas y conocidas es el caso del Nautilus (molusco en espiral), de ahí que se conozca como espiral áurea.

 En un post anterior hablé de la estrecha relación entre el número de oro y la sucesión de Fibonacci, ambas presentes en múltiples fenómenos de la naturaleza, por ejemplo, los girasoles cuentan con dos series de espirales que salen del centro (una en cada sentido), 21 en un sentido y 34 en el otro, números que se extraen de la famosa sucesión.
En un post anterior hablé de la estrecha relación entre el número de oro y la sucesión de Fibonacci, ambas presentes en múltiples fenómenos de la naturaleza, por ejemplo, los girasoles cuentan con dos series de espirales que salen del centro (una en cada sentido), 21 en un sentido y 34 en el otro, números que se extraen de la famosa sucesión.
 ¿Casualidad?. No, matemáticas, y es que la naturaleza es sabia. Según vas realizando los cocientes de los términos de la sucesión de Fibonacci, observarás, que cada vez se aproxima más y más al número de oro. Anecdotas y ejemplos hay miles y ya me está quedando un post de lo más largo y no quiero resultar pesado, sólo deciros que dicha proporción se sigue utilizando en la actualidad, por considerarse ideal, como mencioné antes, nuestro famoso DNI está en proporción áurea.
¿Casualidad?. No, matemáticas, y es que la naturaleza es sabia. Según vas realizando los cocientes de los términos de la sucesión de Fibonacci, observarás, que cada vez se aproxima más y más al número de oro. Anecdotas y ejemplos hay miles y ya me está quedando un post de lo más largo y no quiero resultar pesado, sólo deciros que dicha proporción se sigue utilizando en la actualidad, por considerarse ideal, como mencioné antes, nuestro famoso DNI está en proporción áurea. Ya véis, el número de oro, sigue presente en nuestro arte más actual, nuestro desaparecido genio Salvador Dalí, por ejemplo, lo utilizó para algunas de sus obras y se seguirá utilizando en generaciones futuras, por ser considerado un número mágico.
Ya véis, el número de oro, sigue presente en nuestro arte más actual, nuestro desaparecido genio Salvador Dalí, por ejemplo, lo utilizó para algunas de sus obras y se seguirá utilizando en generaciones futuras, por ser considerado un número mágico. Os dejo con un par de videos en los que podéis informaros un poco más sobre este fascinante número.
Os dejo con un par de videos en los que podéis informaros un poco más sobre este fascinante número.viernes, 16 de mayo de 2008
MAFALDA Y LA GEOMETRÍA
 Os dejo con una tira cómica de la siempre genial Mafalda y a ver si subo más cositas, que últimamente he tenido el blog un poco abandonado por falta de tiempo... He colgado también nuevos links en el margen, así como una película muy buena la cual os recomiendo (eso si a partir de 3º E.S.O. en adelante), es de hace unos 10 años ya, pero es muy buena.
Os dejo con una tira cómica de la siempre genial Mafalda y a ver si subo más cositas, que últimamente he tenido el blog un poco abandonado por falta de tiempo... He colgado también nuevos links en el margen, así como una película muy buena la cual os recomiendo (eso si a partir de 3º E.S.O. en adelante), es de hace unos 10 años ya, pero es muy buena.martes, 29 de abril de 2008
ESTIMACIÓN DE LOS "PUNTOS DE FEKETE"

"Científicos españoles resuelven uno de los grandes retos matemáticos: La estimación de los "puntos de Fekete" tendrá aplicaciones en Física y Medicina."
Un equipo de investigadores de la Universidad Politécnica de Cataluña (UPC) ha resuelto uno de los "enigmas" matemáticos más enrevesados, que desde hace un siglo se resistía a científicos de todo el mundo. Se trata del denominado problema de los puntos de Fekete, que plantea cómo debe distribuirse un número finito de puntos - partículas - sobre una esfera para obtener una configuración estable. Cuanto menos es la energía potencial del conjunto de puntos, menor será el caos de dicho conjunto y, por consiguiente, más estable será la configuración.
El reto, a falta de la validación de la comunidad científica en un próximo congreso, ha sido resuelto por Enrique Bendito, Andrés Encinas, Ángeles Carmona y José M. Gesto, con la ayuda del superordenador Finisterrae, emplazando en el Centro de Supercomputación de Galicia (Santiago de Compostela) y considerado el de mayor memoria compartida de Europa. El trabajo con el ordenador requirió en febrero unas 350.000 horas de cálculo, algo que con un ordenador doméstico hubiese llevado cuarenta años de trabajo.
Los puntos de Fekete estaban clasificados en el número 7 de la lista de problemas del destacado matemático Stephen Smale, que agrupa los 18 problemas de mayor relevancia y dificultad en la actualidad.
Los matemáticos de la UPC han logrado resolver el posicionamiento de decenas de miles de puntos en 50 millones de combinaciones, cuando investigadores anteriores no habían superado los dos mil puntos. La solución del problema tendrá aplicaciones en la formación de moléculas, estructuras cristalinas, diseño de proteínas, dinámica de gases...
Para ver el estudio completo, consulta el pdf, aquí.
El reto, a falta de la validación de la comunidad científica en un próximo congreso, ha sido resuelto por Enrique Bendito, Andrés Encinas, Ángeles Carmona y José M. Gesto, con la ayuda del superordenador Finisterrae, emplazando en el Centro de Supercomputación de Galicia (Santiago de Compostela) y considerado el de mayor memoria compartida de Europa. El trabajo con el ordenador requirió en febrero unas 350.000 horas de cálculo, algo que con un ordenador doméstico hubiese llevado cuarenta años de trabajo.
Los puntos de Fekete estaban clasificados en el número 7 de la lista de problemas del destacado matemático Stephen Smale, que agrupa los 18 problemas de mayor relevancia y dificultad en la actualidad.
Los matemáticos de la UPC han logrado resolver el posicionamiento de decenas de miles de puntos en 50 millones de combinaciones, cuando investigadores anteriores no habían superado los dos mil puntos. La solución del problema tendrá aplicaciones en la formación de moléculas, estructuras cristalinas, diseño de proteínas, dinámica de gases...
Para ver el estudio completo, consulta el pdf, aquí.
sábado, 19 de abril de 2008
LOS PUENTES DE KÖNIGSBERG
 Königsberg fue una popular y rica cuidad de la Prusia Oriental, hoy en día su nombre es Kaliningrado y pertece a Rusia, se encuentra a orillas del mar Báltico y a unos 50 km de la frontera con Polonia.
Königsberg fue una popular y rica cuidad de la Prusia Oriental, hoy en día su nombre es Kaliningrado y pertece a Rusia, se encuentra a orillas del mar Báltico y a unos 50 km de la frontera con Polonia.En esta ciudad se juntan dos ríos, formando una isla en su confluencia. Siete puentes unían (ya no, pues la ciudad fue parcialmente destruida durante la segunda Guerra Mundial) las diferentes partes de la ciudad, como se aprecia en el mapa de la época. En el siglo XVIII se hizo popular como adivinanza/pasatiempo averiguar si era posible cruzar los siete puentes de la ciudad pasando sólo una vez por cada uno de ellos.
Esta ciudad es conocida también por ser la cuna del filósofo Immanuel Kant (1724 - 1804), pero en la historía de las Matemáticas es famosa por la disposición de sus puentes que dió lugar a este juego, precisamente en la época de Kant, que atrajo la atención de los más famosos matemáticos del momento.
Este problema, por supuesto, puede resolverse mediante un estudio exhaustivo de todos los posibles itineriarios. Pero en las matemáticas nos interesamos por generalizar el problema y buscar una solución sencilla y válida para todos los posibles mapas de ciudades, e incluso objetos más generales.
 En 1736, el gran matemático suizo afincado en San Petersburgo, Leonhard Euler, publicó su "Solutio problematis ad geometriam situs pertinentis", un artículo en el que resolvía el problema en el caso general. Este trabajo es considerado como en el nacimiento de la Teoría de Grafos, utilizada hoy en día en un sinfín de aplicaciones, y también uno de las primeras apariciones de una "nueva Geometría" en la que importan sólo las propiedades estructurales de un objeto y no sus medidas. A esto se refieren las palabras "geometrian situs" en el título de Euler, palabras que hoy se traducen como Topología.
En 1736, el gran matemático suizo afincado en San Petersburgo, Leonhard Euler, publicó su "Solutio problematis ad geometriam situs pertinentis", un artículo en el que resolvía el problema en el caso general. Este trabajo es considerado como en el nacimiento de la Teoría de Grafos, utilizada hoy en día en un sinfín de aplicaciones, y también uno de las primeras apariciones de una "nueva Geometría" en la que importan sólo las propiedades estructurales de un objeto y no sus medidas. A esto se refieren las palabras "geometrian situs" en el título de Euler, palabras que hoy se traducen como Topología.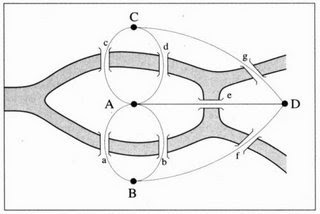 La primera observación es que el problema se puede reformular como sigue. Dado el siguiente
La primera observación es que el problema se puede reformular como sigue. Dado el siguiente "grafo" con cuatro vértices y siete aristas, ¿es posible recorrerlo entero sin pasar dos veces por la misma arista?. En el grafo, los cuatro vértices representan las cuatro partes en que los ríos separan la ciudad, y las siete aristas representan los puentes. Dicho de otro modo, que resulte más familiar a los aficcionados de los pasatiempos: ¿es posible realizar el dibujo del grafo sin levantar el lápiz del papel y sin pasar dos veces por la misma arista? (Se permite pasar dos veces por el mismo vértice).
"grafo" con cuatro vértices y siete aristas, ¿es posible recorrerlo entero sin pasar dos veces por la misma arista?. En el grafo, los cuatro vértices representan las cuatro partes en que los ríos separan la ciudad, y las siete aristas representan los puentes. Dicho de otro modo, que resulte más familiar a los aficcionados de los pasatiempos: ¿es posible realizar el dibujo del grafo sin levantar el lápiz del papel y sin pasar dos veces por la misma arista? (Se permite pasar dos veces por el mismo vértice).La respuesta de Euler es extremadamente simple. Supongamos que, efectivamente, es posible realizar el dibujo sin levantar el lápiz del papel. Al realizar el dibujo, en cada vértice intermedio que atravesemos entraremos por una arista y saldremos por otra. En particular, el número de aristas que confluyen en cada vértice del grafo, exceptuando quizás los vértices inicial y final del dibujo, ha de ser par. Si llamamos "valencia" de cada vértice al número de aristas que confluyen en él, lo dicho anteriormente significa que para que el problema tenga solución es necesario que en el grafo haya como mucho dos vértices de valencia par. En el caso del grafo de Königsberg los cuatro vértices tienen valencia impar, así que el problema no tiene solución. Q.E.D.
lunes, 7 de abril de 2008
EL INVENTOR DEL AJEDREZ
 Como continuación al post anterior en el que hablaba de progresiones, hoy nos centramos en las Progresiones Geométricas, las cuales siguen un crecimiento exponencial, por lo que los términos de la progresión se disparan desmesuradamente (en el caso creciente) y se anula rápidamente en el caso (decreciente).
Como continuación al post anterior en el que hablaba de progresiones, hoy nos centramos en las Progresiones Geométricas, las cuales siguen un crecimiento exponencial, por lo que los términos de la progresión se disparan desmesuradamente (en el caso creciente) y se anula rápidamente en el caso (decreciente).Un claro ejemplo de crecimiento exponencial es la propagación de virus como el de la gripe, dando alcance a un gran número de personas sobre la faz del planeta, en unas cuantas semanas, así como otros sucesos naturales...

Pero hoy os voy a contar la famosa leyenda del Inventor del Ajedrez, dice así la historia, el rey de Persia aburrido en los ratos muertos, de repente quedó fascinado por el juego del ajedrez, el cual le prensentó un inventor ingenioso e inteligente. Se cuenta que quedó tan agradecido que el rey ofreció al matemático oriental lo que deseara.
El inventor contestó:
- Me conformo con 1 grano de trigo por la primera casilla del tablero, 2 por la segunda, 4 por la tercera, 8 por la cuarta y así hasta la casilla 64 del tablero.
(Es decir la suma de los 64 primero términos de una P.G. de razón 2 y cuyo primer término es 1)
El rey se mofó pensando la minucia que le estaba pidiendo y solicitando a su visir que preparara el premio solicitado, hizo los cálculos y se dió cuenta que era imposible cumplir la orden, pues la suma de los granos de las 64 casillas era nada menos que la cantidad de:
18.446.744.073.709.551 616 granos
(En cada kilogramo de trigo caben aproximadamente unos 28 220 granos, por lo que el resultado sería de unas 653 676 260 585 toneladas; que ocuparían un depósito en forma de cubo de algo más de 11′5 kilómetros de lado.
Para producir tal cantidad de trigo se necesitaría estar cultivando la Tierra (incluidos los mares), durante ocho años)
Para producir tal cantidad de trigo se necesitaría estar cultivando la Tierra (incluidos los mares), durante ocho años)

Hay una segunda parte de la historia, que es la siguiente, debido al bochorno del rey de tener que aceptar que no tenía granos suficientes para pagarle, consulto a otro hombre inteligente e ingenioso de su corte para que le sacara del apuro.
Y este le propuso lo siguiente:
- Para que vea el inventor cuan generoso eres, ofrécele no sólo la suma de los 64 primeros términos sino la suma infinita.
A lo que el rey exclamó:
- ¡Estás loco!. Si no tengo para pagarle como voy a hacer para prolongar la suma hasta el infinito, serían infinitos granos...
Pero el ayudante ingenioso le dijo:
- Llévame ante el inventor y confía en mí, todo va a salir bien!
 Una vez allí reunidos, el ingenioso ayudante le propuso al inventor, que el rey estaba tan contento y feliz con el juego del ajedrez y se mostraba tan generoso, que no sólo se ofrecía a darle la suma de las 64 casillas, sino la suma infinita. A lo que, encogiéndose de hombros el inventor aceptó. Y el ayudante del rey empezó a explicar:
Una vez allí reunidos, el ingenioso ayudante le propuso al inventor, que el rey estaba tan contento y feliz con el juego del ajedrez y se mostraba tan generoso, que no sólo se ofrecía a darle la suma de las 64 casillas, sino la suma infinita. A lo que, encogiéndose de hombros el inventor aceptó. Y el ayudante del rey empezó a explicar:
Llamemos
Y este le propuso lo siguiente:
- Para que vea el inventor cuan generoso eres, ofrécele no sólo la suma de los 64 primeros términos sino la suma infinita.
A lo que el rey exclamó:
- ¡Estás loco!. Si no tengo para pagarle como voy a hacer para prolongar la suma hasta el infinito, serían infinitos granos...
Pero el ayudante ingenioso le dijo:
- Llévame ante el inventor y confía en mí, todo va a salir bien!
 Una vez allí reunidos, el ingenioso ayudante le propuso al inventor, que el rey estaba tan contento y feliz con el juego del ajedrez y se mostraba tan generoso, que no sólo se ofrecía a darle la suma de las 64 casillas, sino la suma infinita. A lo que, encogiéndose de hombros el inventor aceptó. Y el ayudante del rey empezó a explicar:
Una vez allí reunidos, el ingenioso ayudante le propuso al inventor, que el rey estaba tan contento y feliz con el juego del ajedrez y se mostraba tan generoso, que no sólo se ofrecía a darle la suma de las 64 casillas, sino la suma infinita. A lo que, encogiéndose de hombros el inventor aceptó. Y el ayudante del rey empezó a explicar:Llamemos
S = 1 + 2 + 4 + 8 + 16 + ... (a la suma infinita)
ahora la multiplicamos por 2, de manera que tenemos 2S,
A continuación hacemos 2S - 1S,
2S= 2 + 4 + 8 + 16 + 32 + ...
A continuación hacemos 2S - 1S,
2S = 2 + 4 + 8 + 16 + 32 + ...
-1S = - 1 - 2 - 4 - 8 - 16 - ...
______________________
S = -1
______________________
S = -1
De manera que observamos que 2 y -2 se cancelan, así 4 y -4, e igual hasta el infinito... de manera que al final, S = -1. No sólo ya no le tenía que pagar al inventor, sino que encima este le debía un grano. ¡Sorprendente! (Pues es lo que tiene jugar con el infinito, este tipo de casos se les conoce como paradojas del infinito)
miércoles, 5 de marzo de 2008
FIBONACCI Y SU FAMOSA SUCESIÓN
 Leonardo de Pisa (1170 - 1250), también conocido como Fibonacci, fue uno de los Matemáticos más importantes de la Edad Media en Europa. Hizo importantes contribuciones a la aritmética, al álgebra y la geometría.
Leonardo de Pisa (1170 - 1250), también conocido como Fibonacci, fue uno de los Matemáticos más importantes de la Edad Media en Europa. Hizo importantes contribuciones a la aritmética, al álgebra y la geometría.Por lo que más se le conoce actualmente es por su famosa sucesión, seguro que la has visto en más de una ocasión:
1 ,1, 2, 3, 5, 8, 13, 21, ...
Como ya te habrás dado cuenta, esta sucesión empieza con dos unos, cualquier término de la sucesión se obtiene de sumar los dos anteriores y la sucesión es infinita. Y ¿por qué es tan famosa esta sucesión?. Pues porque la naturaleza es sabia y se ha comprobado que múltiples patrones de ella como plantas, animales, ... siguen dicha sucesión... Por ejemplo en la procreación de una pareja de conejos por meses...
 Pero no sólo por esto, por ejemplo, si se divide cada número de la sucesión entre su vecino inmediato de la derecha se obtiene la sucesión de fracciones llamadas cocientes de Fibonacci (1/1, 1/2, 2/3, 3/5, 5/8, 8/13, ...). A medida que avanzan estos cocientes hacia infinito el resultado tiende al número:
Pero no sólo por esto, por ejemplo, si se divide cada número de la sucesión entre su vecino inmediato de la derecha se obtiene la sucesión de fracciones llamadas cocientes de Fibonacci (1/1, 1/2, 2/3, 3/5, 5/8, 8/13, ...). A medida que avanzan estos cocientes hacia infinito el resultado tiende al número:
 Este número es de los más famosos en el mundo matemático, se conoce con Número de Oro (hablaré largo y tendido de este en otro post que estoy preparando) y tiene que ver con la famosa Proporción Áurea, símbolo de belleza natural, y utilizada desde los griegos hasta nuestros días en cantidad de construcciones, obras de arte, cuadros o más sencillamente nuestro DNI. Proporción que se da por supuesto en cantidad de ejemplos naturales, pero como he dicho, da para mucho este tema y prefiero dejarlo para otro post, sólo dejo una muestra de la estrecha relación de esta sucesión, con la proporción áurea y la naturaleza...
Este número es de los más famosos en el mundo matemático, se conoce con Número de Oro (hablaré largo y tendido de este en otro post que estoy preparando) y tiene que ver con la famosa Proporción Áurea, símbolo de belleza natural, y utilizada desde los griegos hasta nuestros días en cantidad de construcciones, obras de arte, cuadros o más sencillamente nuestro DNI. Proporción que se da por supuesto en cantidad de ejemplos naturales, pero como he dicho, da para mucho este tema y prefiero dejarlo para otro post, sólo dejo una muestra de la estrecha relación de esta sucesión, con la proporción áurea y la naturaleza...

Os dejo con un par de juegos matemáticos relacionados con la sucesión de Fibonacci:
1º. Una falacia geométrica
Traza un rectángulo cuyos lados midan 8 y 21. Recórtalo por las marcas que se muestran en la figura. Con las piezas que queden construye un cuadrado cuyo lado mida 13.

- Cálcula el área del rectángulo.
- Cálcula el área del cuadrado.
¿Son iguales estas áreas?. ¿Qué está sucediendo?, ¿es correcto el resultado que obtuviste?. ¿Tendrá algo que ver que 8, 13 y 21 son números consecutivos de la sucesión de Fibonacci?.
2º. Truco de Fibonacci
 Piensa en dos números cualesquiera y construye, empezando con esos números, una sucesión como la de Fibonacci, es decir que cada término sea la suma de los dos anteriores.
Piensa en dos números cualesquiera y construye, empezando con esos números, una sucesión como la de Fibonacci, es decir que cada término sea la suma de los dos anteriores.
La suma de los diez primeros términos de tu sucesión será once veces el séptimo término. Esto sucede en la sucesión de Fibonacci y en cualquier otra que se construya de la misma manera. ¿Sorprendente verdad?.
 Pero no sólo por esto, por ejemplo, si se divide cada número de la sucesión entre su vecino inmediato de la derecha se obtiene la sucesión de fracciones llamadas cocientes de Fibonacci (1/1, 1/2, 2/3, 3/5, 5/8, 8/13, ...). A medida que avanzan estos cocientes hacia infinito el resultado tiende al número:
Pero no sólo por esto, por ejemplo, si se divide cada número de la sucesión entre su vecino inmediato de la derecha se obtiene la sucesión de fracciones llamadas cocientes de Fibonacci (1/1, 1/2, 2/3, 3/5, 5/8, 8/13, ...). A medida que avanzan estos cocientes hacia infinito el resultado tiende al número: Este número es de los más famosos en el mundo matemático, se conoce con Número de Oro (hablaré largo y tendido de este en otro post que estoy preparando) y tiene que ver con la famosa Proporción Áurea, símbolo de belleza natural, y utilizada desde los griegos hasta nuestros días en cantidad de construcciones, obras de arte, cuadros o más sencillamente nuestro DNI. Proporción que se da por supuesto en cantidad de ejemplos naturales, pero como he dicho, da para mucho este tema y prefiero dejarlo para otro post, sólo dejo una muestra de la estrecha relación de esta sucesión, con la proporción áurea y la naturaleza...
Este número es de los más famosos en el mundo matemático, se conoce con Número de Oro (hablaré largo y tendido de este en otro post que estoy preparando) y tiene que ver con la famosa Proporción Áurea, símbolo de belleza natural, y utilizada desde los griegos hasta nuestros días en cantidad de construcciones, obras de arte, cuadros o más sencillamente nuestro DNI. Proporción que se da por supuesto en cantidad de ejemplos naturales, pero como he dicho, da para mucho este tema y prefiero dejarlo para otro post, sólo dejo una muestra de la estrecha relación de esta sucesión, con la proporción áurea y la naturaleza...
Os dejo con un par de juegos matemáticos relacionados con la sucesión de Fibonacci:
1º. Una falacia geométrica
Traza un rectángulo cuyos lados midan 8 y 21. Recórtalo por las marcas que se muestran en la figura. Con las piezas que queden construye un cuadrado cuyo lado mida 13.

- Cálcula el área del rectángulo.
- Cálcula el área del cuadrado.
¿Son iguales estas áreas?. ¿Qué está sucediendo?, ¿es correcto el resultado que obtuviste?. ¿Tendrá algo que ver que 8, 13 y 21 son números consecutivos de la sucesión de Fibonacci?.
2º. Truco de Fibonacci
 Piensa en dos números cualesquiera y construye, empezando con esos números, una sucesión como la de Fibonacci, es decir que cada término sea la suma de los dos anteriores.
Piensa en dos números cualesquiera y construye, empezando con esos números, una sucesión como la de Fibonacci, es decir que cada término sea la suma de los dos anteriores. La suma de los diez primeros términos de tu sucesión será once veces el séptimo término. Esto sucede en la sucesión de Fibonacci y en cualquier otra que se construya de la misma manera. ¿Sorprendente verdad?.
- Construye varias sucesiones como la de Fibonacci y comprueba que siempre se cumple el truco.
- Intenta demostrar por qué sucede.
Para los alumnos de 3º E.S.O.
Hemos empezado viendo el concepto de sucesión para pasar posteriormente a las progresiones tanto aritméticas como geométricas, aquí os dejo los apuntes y ejercicios que os anuncié, para que podáis descargarlos cómodamente desde casa. Lo seguiremos trabajando en clase... Ya colgaré anécdotas y cosillas interesantes sobre progresiones en próximos posts... ok?


- Intenta demostrar por qué sucede.
Para los alumnos de 3º E.S.O.
Hemos empezado viendo el concepto de sucesión para pasar posteriormente a las progresiones tanto aritméticas como geométricas, aquí os dejo los apuntes y ejercicios que os anuncié, para que podáis descargarlos cómodamente desde casa. Lo seguiremos trabajando en clase... Ya colgaré anécdotas y cosillas interesantes sobre progresiones en próximos posts... ok?


martes, 4 de marzo de 2008
lunes, 25 de febrero de 2008
DONALD EN EL PAÍS DE LAS MATEMÁTICAS
 Año tras año he puesto a mis alumnos de 2º de E.S.O. un vídeo que llevo guardando como un tesoro desde que me hice casualmente con una copia hace 12 años, eso sí, una copia de copia ya un tanto deteriorada, he buscado sin éxito la posibilidad de una edición en DVD... dándolo por imposible. Hasta que me lo he encontrado, para mi sorpresa, en Youtube (segmentado en 3 partes de 9 minutos cada una), por eso quiero compartirlo con vosotros aquí en este blog.
Año tras año he puesto a mis alumnos de 2º de E.S.O. un vídeo que llevo guardando como un tesoro desde que me hice casualmente con una copia hace 12 años, eso sí, una copia de copia ya un tanto deteriorada, he buscado sin éxito la posibilidad de una edición en DVD... dándolo por imposible. Hasta que me lo he encontrado, para mi sorpresa, en Youtube (segmentado en 3 partes de 9 minutos cada una), por eso quiero compartirlo con vosotros aquí en este blog. Se trata de un corto producido por Walt Disney en 1959, titulado Donald en el País de las Matemáticas, genial como da una visión muy útil de las Matemáticas en la vida real, abarcando su estrecha relación con la música, la naturaleza, los avances tecnológicos, juegos de mesa, deportes, astronomía, etc. Además de llevarnos de viaje a la antigua Grecia para conocer a los Pitagóricos, o a la época de Leonardo DaVinci y su pasión por el número de oro o proporción áurea. O ¿qué tiene que ver el juego del billar con las fracciones?...
Se trata de un corto producido por Walt Disney en 1959, titulado Donald en el País de las Matemáticas, genial como da una visión muy útil de las Matemáticas en la vida real, abarcando su estrecha relación con la música, la naturaleza, los avances tecnológicos, juegos de mesa, deportes, astronomía, etc. Además de llevarnos de viaje a la antigua Grecia para conocer a los Pitagóricos, o a la época de Leonardo DaVinci y su pasión por el número de oro o proporción áurea. O ¿qué tiene que ver el juego del billar con las fracciones?... Vaya!, para mí, una joya audiovisual de 27 minutos, que cierra con un broche de oro:
Vaya!, para mí, una joya audiovisual de 27 minutos, que cierra con un broche de oro:"Las matemáticas son el alfabeto con el cual Dios ha escrito el Universo"
Galileo Galilei
Galileo Galilei
Pues con ello os dejo, ya digo, está partido en 3 vídeos de 9 minutos cada uno, los pongo en orden para que los podáis visionar uno detrás de otro, espero que os guste!
Suscribirse a:
Comentarios (Atom)

















